Interpretation der Doppler Geschwindigkeit

anhand der ETH Doppler Radar CAPPI's.

Reflektivität (Echo-Stärke) in 5km Höhe:

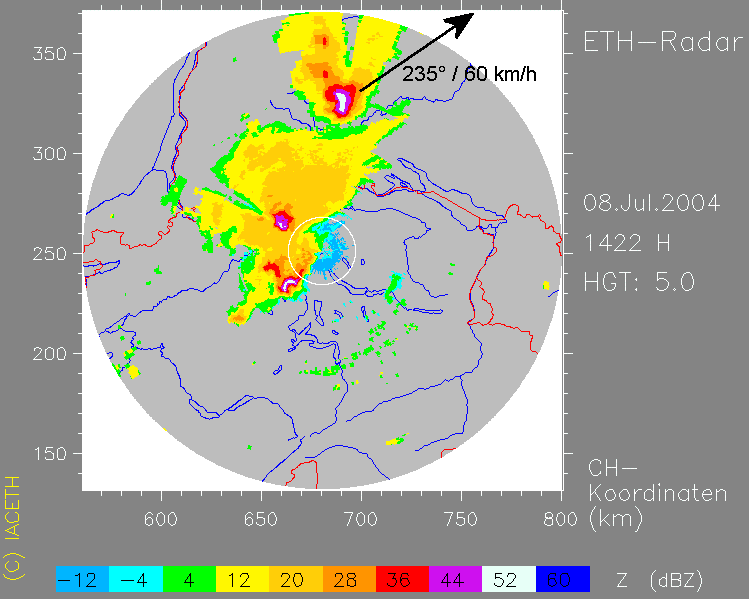
Die Gewitterzelle (Superzelle) im Schwarzwald zieht mit rund 60 km/h aus einer Richtung von 235° auf den Beobachter zu, der sich in ihrer Zugbahn befindet.


Doppler-Geschwindigkeit in 5km Höhe:

Da im CAPPI die Messwerte auf einer konstanten Höhe (5km) angezeigt werden, eignen sich diese Radarbilder besonders gut um Superzellen zu verifizieren. Die Mesozyklone einer Superzelle ist in dieser Höhe meist am Besten zu erkennen. Im eingezeichneten Fall ist die Mesozyklone mit ihren beiden Zentren gut zu erkennen. Damit es eine Mesozyklone ist muss es ein Minimum und ein Maximum an Doppler-Geschwindigkeit im gleichen Abstand vom Radar aus gesehen vorhanden sein, was hier der Fall ist. Dass wir es mit einer Superzelle zu tun haben wissen wir jetzt definitiv.
Um herauszufinden ob es eine Zyklonale oder Antizyklonale Mesozyklone ist, vergleicht man am Besten den Farbverlauf in den beiden Zentren der Mesozyklone. In diesem Beispiel haben wir auf der rechten Seite den Verlauf von Blau nach Gelb, was auf der Skala von Links nach Rechts ist, also "Away" (vom Radar weg). Auf der Linken Seite von Rot nach Orange, was auf der Farbskala von Rechts nach Links ist, also "Towards" (auf das Radar zu).



Die Skala auf dem Bild der Doppler-Geschwindigkeit beschränkt sich auf den Bereich -14.4m/s bis +14.4m/s. Je nachdem wie schnell sich die Superzelle fortbewegt (hier 60 km/h), oder sich die Mesozyklone dreht können Werte vorhanden sein, die Ausserhalb dieser Skala liegen und in dem Fall werden die Farben "gefaltet" dargestellt, d.h. die Skala wird einfach vergrössert, indem man mit der Farbskala wieder am anderen Ende beginnt (siehe Grafik).
Mit der vergrösserten Farbskala hat man nun aber mehrere Möglichkeiten, wo es zutreffende Farben für die im Doppler-Bild eingezeichneten Echos gibt. Hier ist ein wenig Interpretation nötig um auf die richtigen Werte zu kommen. Wir wissen von der Superzelle, dass sie sich mit 60 km/h nach Nordosten, also vom Radar weg, bewegt. Daher sollte generell eine Skala in der "Away" Richtung in Frage kommen. Somit kommt man auf die Werte +4.8 m/s und +40.0 m/s für die Mesozyklone (siehe Grafik).



Die 4.8 m/s (~17 km/h) und 40.0 m/s (144 km/h) entsprechen aber noch nicht den realen Werten der Mesozyklone, sondern es muss noch die Geschwindigkeit und Zugrichtung der Superzelle (60 km/h, 235°) miteinbezogen werden. Hier kommt etwas Trigonometrie mit ins Spiel, da die gemessenen Geschwindigkeiten der Mesozyklone vom Radar aus gesehen sind und die Zugrichtung/Geschwindigkeit der Superzelle vom Beobachter aus, der sich für die Berechnung mal einfach direkt unter das Zentrum der Mesozyklone stellt (Reale Nachahmung bitte nur mit entsprechender Ausrüstung).



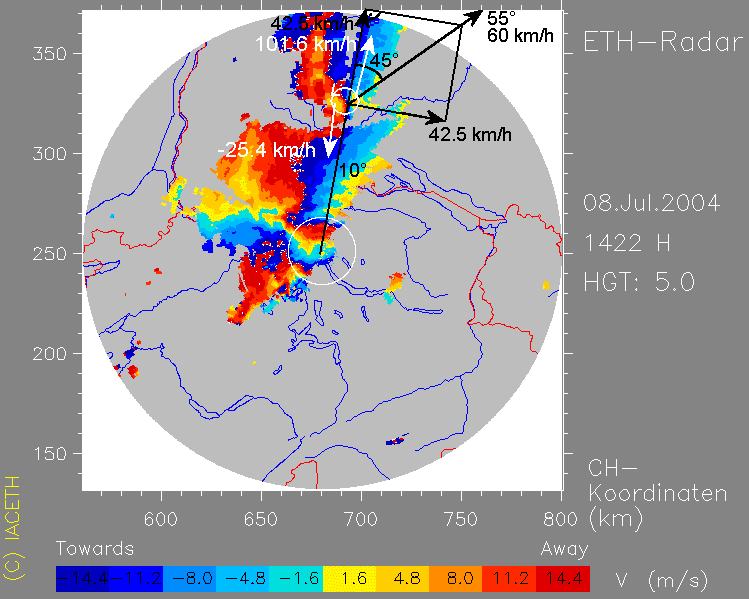
Macht man nun ein Koordinatensystem mit dem Zentrum der Superzelle als Nullpunkt, so zieht die Superzelle in eine Richtung von 55°, während das Radar in eine Richtung von 10° misst. So kommen wir auf einen Winkel von 45° zwischen Radarmessung und realer Zugrichtung, Mittels Kosinussatz kommen wir nun auf den gesuchten Wert um den wir die Beiden gemessenen Werte der Mesozyklone anpassen müssen, um die realen Werte zu erhalten.

cos(45°) = x / 60 km/h
--> x = 42.4 km/h

Da die berechneten 42.4 km/h von Radar weg gerichtet sind müssen sie von den gemessenen Werten der Mesozyklone subtrahiert werden. Das ergibt dann die Werte von -25.4 km/h bzw. +101.6 km/h für die Mesozyklone.